Embark on a captivating journey into the realm of graphing radical functions as we delve into the intricacies of this intriguing mathematical concept. Graphing Radical Functions Quiz Part 1 sets the stage for an immersive exploration, providing a comprehensive understanding of radical functions, their transformations, and their practical applications.
This introductory segment lays the foundation for a deeper understanding of the topic, ensuring that readers are well-equipped to navigate the subsequent sections with confidence.
Graphing Radical Functions: Understanding the Basics: Graphing Radical Functions Quiz Part 1
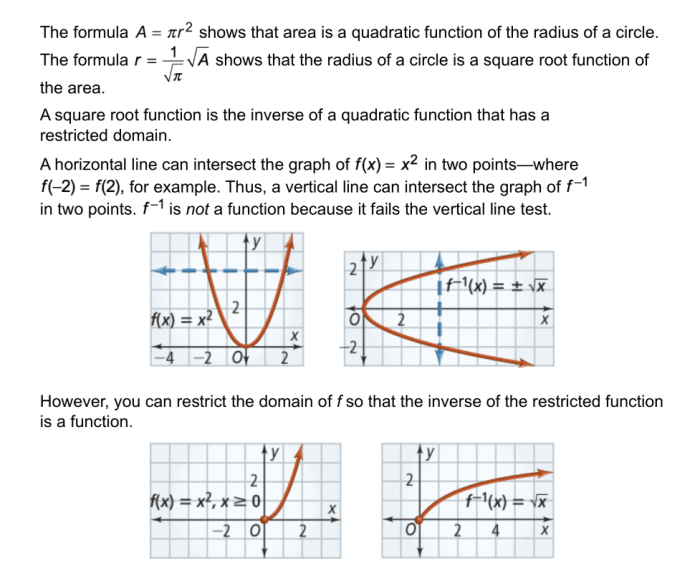
Radical functions are a type of mathematical function that involve the square root of a variable. They are commonly used to model real-world phenomena, such as the trajectory of a projectile or the growth of a population.
There are two main types of radical functions: square root functions and cube root functions. Square root functions have the form f(x) = √x, while cube root functions have the form f(x) = ∛x.
The graphs of radical functions are typically smooth curves that have a characteristic “V” shape. The vertex of the graph is located at the point (0, 0), and the graph extends infinitely in both the positive and negative directions.
Here are some examples of radical functions with their corresponding graphs:
- f(x) = √x: The graph of this function is a “V” shaped curve that opens up.
- f(x) = -√x: The graph of this function is a “V” shaped curve that opens down.
- f(x) = ∛x: The graph of this function is a “V” shaped curve that is steeper than the graph of f(x) = √x.
- f(x) = -∛x: The graph of this function is a “V” shaped curve that is steeper than the graph of f(x) = √x and opens down.
Transformations of Radical Functions, Graphing radical functions quiz part 1
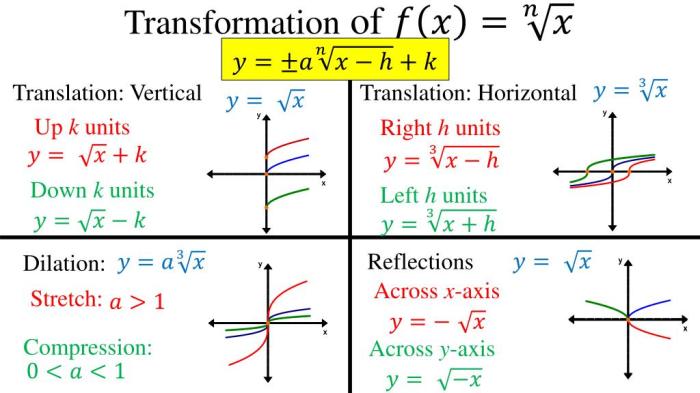
Radical functions can be transformed in the same way as other types of functions. Translations, reflections, and stretches can all be used to change the shape and position of the graph of a radical function.
- Translations:Translating a radical function vertically or horizontally will shift the graph up, down, left, or right.
- Reflections:Reflecting a radical function over the x-axis will flip the graph upside down. Reflecting a radical function over the y-axis will flip the graph left to right.
- Stretches:Stretching a radical function vertically will make the graph taller or shorter. Stretching a radical function horizontally will make the graph wider or narrower.
Here are some examples of transformed radical functions with their corresponding graphs:
- f(x) = √(x + 2): The graph of this function is the graph of f(x) = √x translated 2 units to the left.
- f(x) = -√(x – 3): The graph of this function is the graph of f(x) = √x translated 3 units to the right and reflected over the x-axis.
- f(x) = 2√x: The graph of this function is the graph of f(x) = √x stretched vertically by a factor of 2.
- f(x) = √(0.5x): The graph of this function is the graph of f(x) = √x stretched horizontally by a factor of 0.5.
Q&A
What is the purpose of Graphing Radical Functions Quiz Part 1?
This quiz serves as an introduction to the topic, providing a comprehensive overview of the basics of graphing radical functions.
What topics are covered in Graphing Radical Functions Quiz Part 1?
This quiz covers the concept of radical functions, their different types, and examples of radical functions with graphs.
How can I prepare for Graphing Radical Functions Quiz Part 1?
To prepare for this quiz, it is recommended to review the provided Artikel and familiarize yourself with the concepts of radical functions and their graphs.