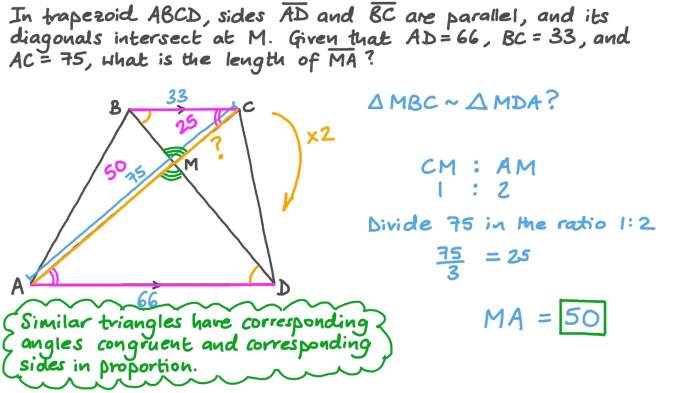
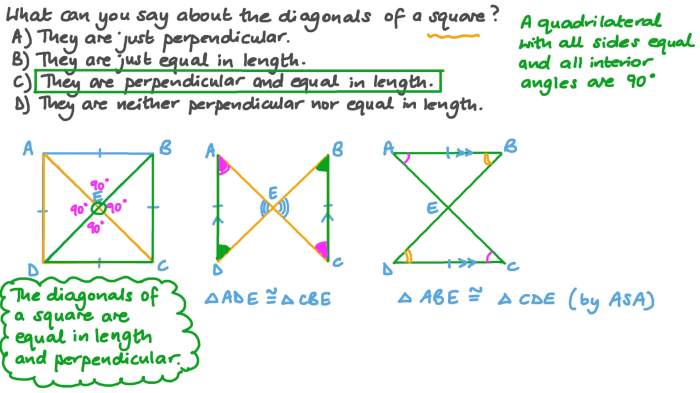
The _____ of a square are both congruent and perpendicular. – The properties of a square, including its congruent sides and perpendicular angles, define its unique geometric characteristics. Understanding these properties is essential for comprehending the behavior and applications of squares in various fields.

A square is a two-dimensional shape with four equal sides and four right angles. The congruence of its sides implies that all four sides have the same length, while the perpendicularity of its angles means that each pair of adjacent sides forms a 90-degree angle.

Properties of Squares: The _____ Of A Square Are Both Congruent And Perpendicular.

A square is a two-dimensional shape with four equal sides and four right angles. These unique characteristics define the shape and properties of a square.

Congruent sides refer to sides of equal length, while perpendicular angles are angles that measure exactly 90 degrees. In a square, all four sides are congruent, and all four angles are perpendicular.

Congruent Sides of a Square

Congruent sides mean that all four sides of a square have the same length. This property is essential for defining the shape of a square and distinguishing it from other quadrilaterals.

To determine congruence, measure the lengths of the sides using a ruler or measuring tape. If all four sides have the same measurement, they are congruent.

Perpendicular Angles of a Square, The _____ of a square are both congruent and perpendicular.

Perpendicular angles in a square refer to the four right angles formed at the intersection of the sides. These angles measure exactly 90 degrees.

To determine perpendicularity, use a protractor or a set square. Place the protractor or set square on the angle and check if the measurement reads 90 degrees.

Relationship between Congruent Sides and Perpendicular Angles

The congruence of sides and the perpendicularity of angles in a square are interconnected. The equal lengths of the sides ensure that the angles formed at the vertices are all right angles.

This relationship is governed by geometric principles, such as the Pythagorean theorem and the properties of quadrilaterals. These principles establish the connection between the side lengths and the angles of a square.

Applications of Square Properties

The properties of squares have practical applications in various fields, including architecture, engineering, and design.

• Architecture:Squares are used in the design of buildings, windows, and other architectural elements to create symmetry and balance.
• Engineering:Squares are employed in the construction of bridges, beams, and other structures to ensure stability and strength.
• Design:Squares are incorporated into logos, graphics, and other design elements to convey a sense of order, precision, and stability.

FAQs

What is the difference between a square and a rectangle?

A square is a specific type of rectangle with all four sides equal in length. In contrast, a rectangle has two pairs of parallel sides, but the lengths of the sides can differ.

How can I measure the angles of a square?

You can use a protractor to measure the angles of a square. Place the protractor’s center point on one of the vertices of the square and align its baseline with one of the sides. The angle formed by the two adjacent sides will be 90 degrees.

What are some real-world applications of the properties of squares?

The properties of squares are used in various applications, including architecture, engineering, and design. For example, the congruent sides of a square ensure stability in structures, while the perpendicular angles facilitate precise measurements and alignments.